A Neural Network Based Approach for Approximating Real Roots of Polynomials
Abstract
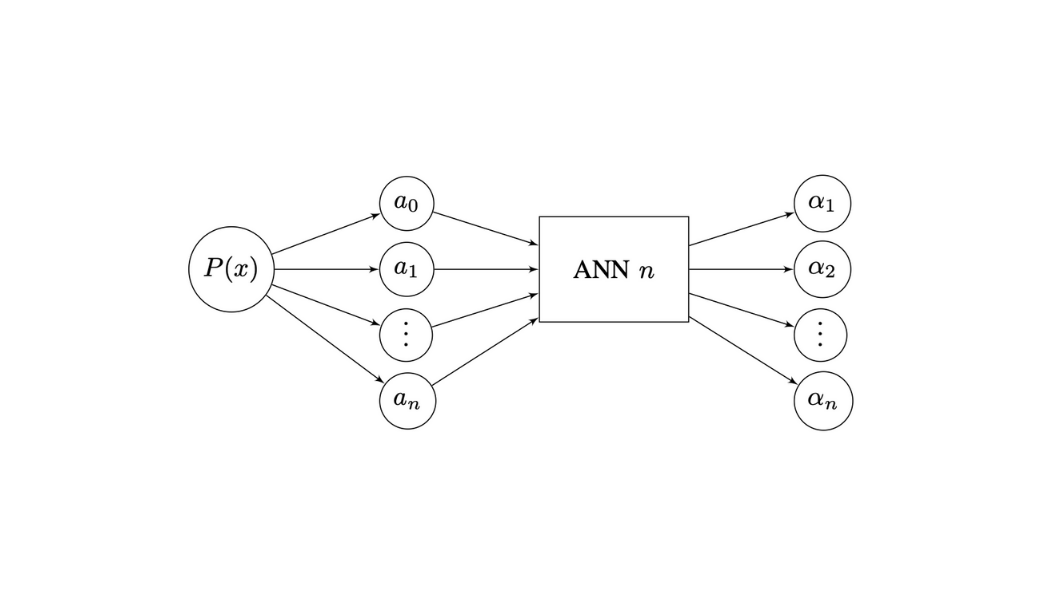
There are many iterative methods for finding all the zeros of a polynomial sequentially or simultaneously. However, the determination of all zeros of a given polynomial by one of the methods that find one zero at a time involves repeated deflations, which leads to the accumulation of rounding errors and inaccurate results. In turn, the simultaneous methods require very good starting approximations for all the zeros in order to converge. In view of these drawbacks, in this work we adopt a different approach based on neural networks for finding the zeros of real polynomials with only real zeros. This approach is tested with random polynomials of different degrees. The results obtained, although preliminary and limited, indicate that this approach seems to be quite robust and promising, and faster when compared with the well known Durand–Kerner method.
More information
- Authors
- Diogo Freitas; Luiz Guerreiro Lopes; Fernando Morgado-Dias
- Date
- 2018
- Conference
- International Conference on Mathematical Applications (ICMA)
- Publisher
- IKnowD
- Conference location
- Funchal, Portugal
- Source
- Link
Citation
@inproceedings{freitas2018,
author = {Freitas, Diogo and Lopes, Luiz Guerreiro and Morgado-Dias, Fernando},
booktitle = {Proceedings of the International Conference on Mathematical Applications (ICMA)},
month = {6},
pages = {9--12},
title = {A Neural network based approach for approximating real roots of polynomials},
year = {2018}
}
